Simulations Lab page
 |
In occasione della Notte dei Ricercatori 2008 abbiamo preparato una pagina speciale contenente delle simulazioni su Caos e Sistemi Complessi commentate in italiano. Cliccate QUI' o sul banner a sinistra se volete dargli un'occhiata... |
|
|---|---|---|
Note: The applets presented in this page require Java Runtime Environment (Java 1.4.1 or higher). It will not run on Windows 95 or Mac OS 8 or 9. Mac users must have OS X 10.2.6 or higher and use a browser that supports Java 1.4. (Safari works, IE does not. Mac OS X comes with Safari. Open Safari and set it as your default web browser under Safari/Preferences/General.) On other operating systems, or if the simulations do not start, you may obtain the latest Java plugin from Sun's Java site. |
||
| Play with these Java applets dedicated to long range models, in particular the Hamiltonian Mean field model, a fully coupled system of inertial rotators showing a complex dynamics due to the long-range nature of the interaction, and to many other topics, among which Conservative and Dissipative Dynamical Systems, Coupled Maps, Electronic Detectors, Complex Networks, Synchronization of Coupled Oscillators, Sociophysics, Neural Networks, etc... | ||
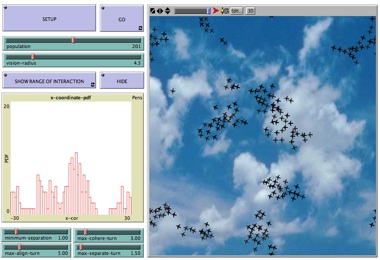
A common features shared by many complex systems is the long range nature of the interaction among their elements. In order to show as such a feature could be crucial for the emergence of a cooperative behavior from a caotic one, let us to start with an unusual example of system with variable range of interaction: clicking on the right you can play with an imaginary flock where the radius of interaction among birds can be varied by the user... have fun!:-) |
||
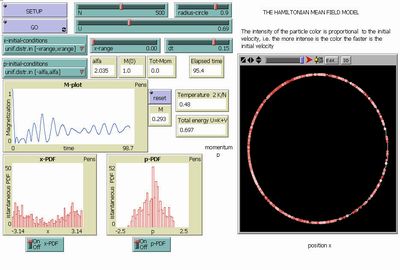
HMF Model - Dynamics on Unit Circle |
HMF Model - Dynamics in Phase Spase |
|
 |
||
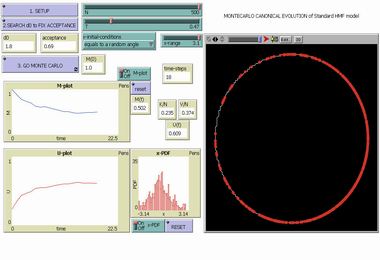
HMF Model - Canonical Monte Carlo |
HMF Model - Contour Plot in Phase Spase |
|
 |
||
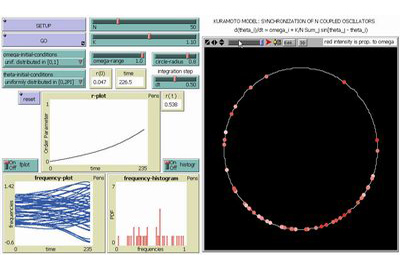
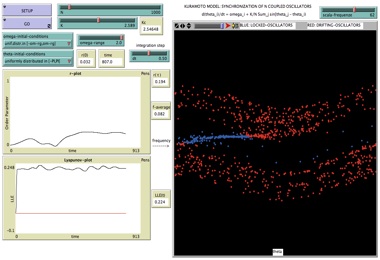
Kuramoto Model |
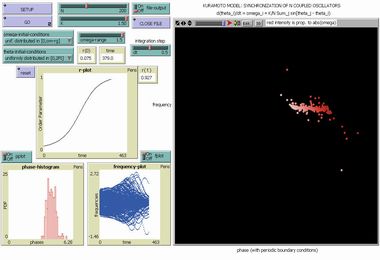
Kuramoto Model in Phase Space |
|
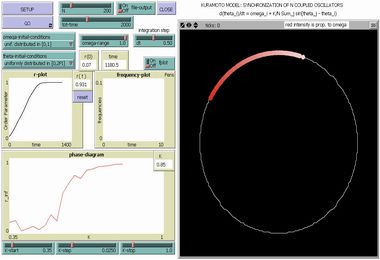
Kuramoto Model - Phase Diagram |
Kuramoto Model - Largest Lyapunov Exponent |
|
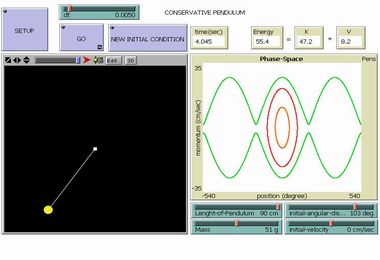
Conservative Pendulum |
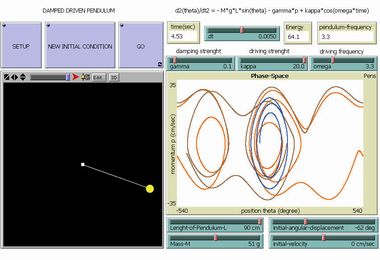
Driven Damped Pendulum |
|
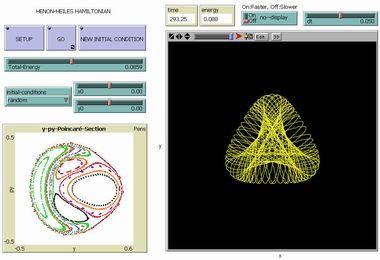
Henon-Heiles Hamiltonian |
Cat Map |
|
Logistic Map and Bifurcation Diagram |
Lyapunov Exponent of Logistic Map |
|
Z-Logistic Map |
Kaneko Coupled Logistic Maps with Noise |
|
q-Entropy and Bifurcations in Quadratic Map |
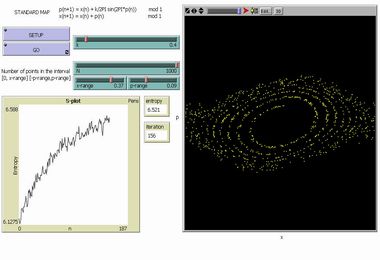
Entropy Growth of N Standard Maps |
|
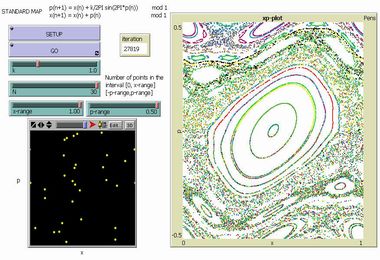
Phase Space of N Standard Maps |
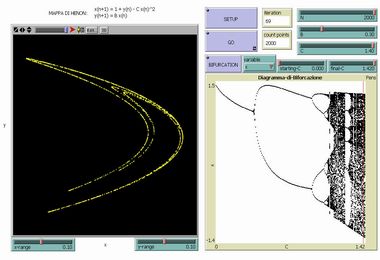
Attractors and Bifurcations in Henon Maps |
|
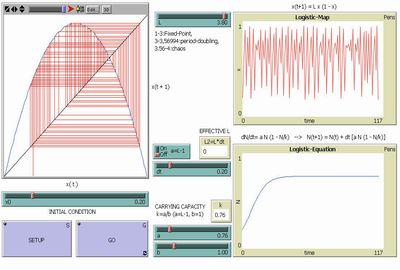
Logistic Map vs Logistic Equation |
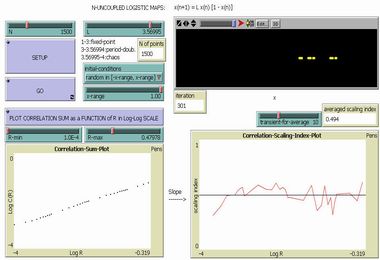
Correlation Dimension in Logistic Map |
|
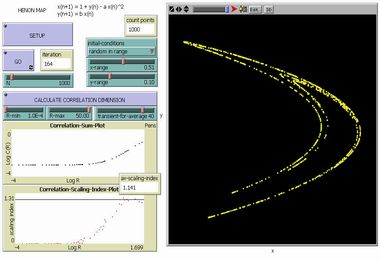
Correlation Dimension in Henon Map |
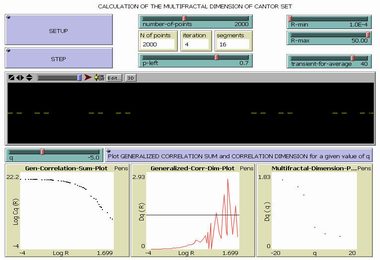
Multifractal Dimension in Cantor Set |
|
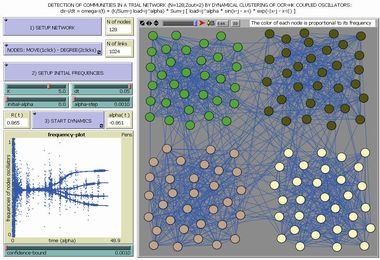
Community Structures on Complex Networks |
Community Structures on Test Networks |
|
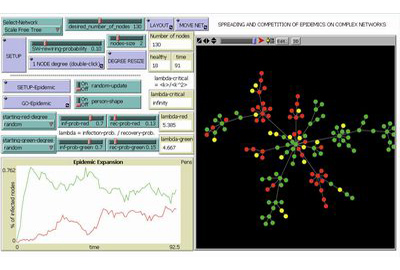
Epidemics on Complex Networks |
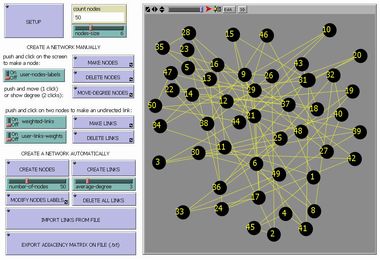
Create your Network |
|
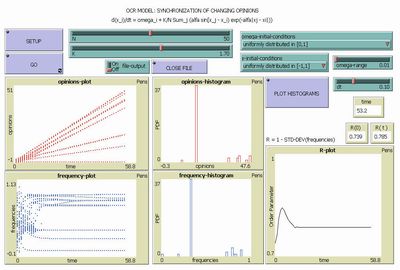
Opinion Changing Rate Model |
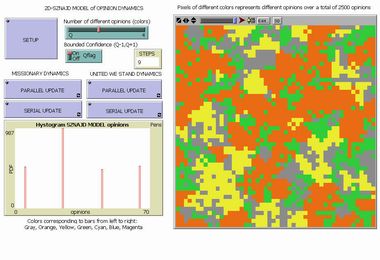
Sznajd-Weron Opinion Dynamics |
|
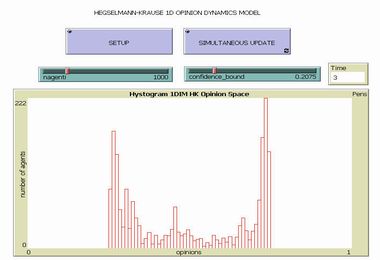
Hegselmann and Krause Opinion Dynamics |
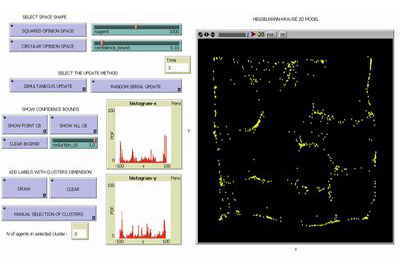
Hegselmann and Krause 2D |
|
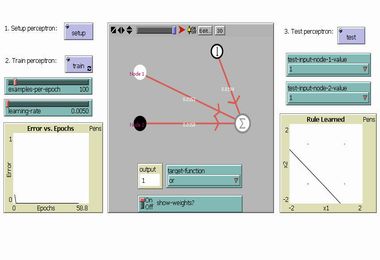
Perceptron (Artificial Neuron) |
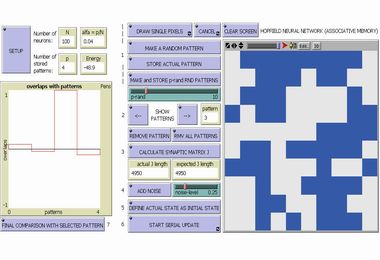
Hopfield Associative Memory |
|
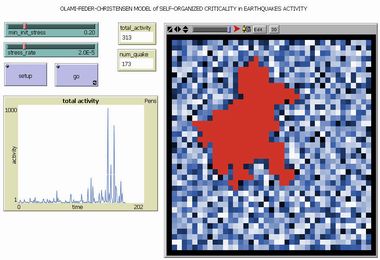
OFC Model of Earthquakes Activity |
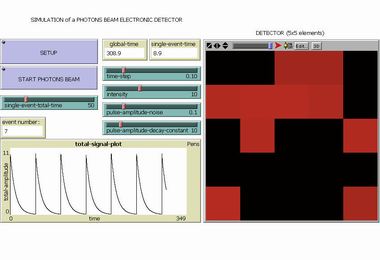
Photons Beam Electronic Detector |